Blogia
Bitneriáceo

Four Corners, again

- Adivínalo. continua en :
Four Corners, again 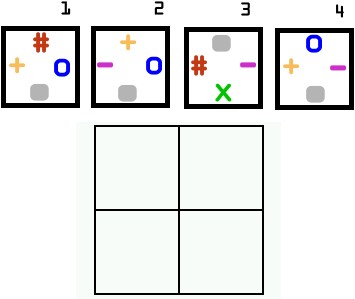Volvemos a las cuatro esquinas, hoy hay que situar las 4 fichas dentro de la cuádruple frontera de forma que a uno y otro lado de cada frontera las figuras que se enfrenten sean iguales.

Visto que eso es muy fácil, para los que quieran ir entrenándose para el IPST la pregunta es ¿cuántas soluciones tendría si se pide lo contrario, es decir que a uno y otro lado de cada frontera las figuras sean distintas?

Las fichas se pueden rotar pero no reflejar.

19 comentarios

pini -

no santiago.
todo el tema viene por raquel machin.
no soy raquel ni pini lópez.

Santiago -

¿pini lópez?

pini -

está bien, pero no penélope.
(me sobra "de la")

alejo -

Yo pensaba llamarte Inés

pini -

alejo seguí adivinando y decime...juana.

alejo -

Toque de maestra,Pini.
Pero ahora estoy más confundido, ¿Sos Pini, Raquel o Sor Pini?

ramtia -

Pini maravilloso, esa si que eres tu.

pini, transmitiendo dormida. -

basta ya hombres necios.
no me acuseis sin razón
sin ver que sois la ocasión
de lo mismo que culpáis.

no me llameis raquel,
machin machin o welch
si con ansia sin igual
solicitáis mi desdén,
por qué queréis que obre bien
si me incitáis al mal?

confesar....no confesaré nada.

p.d.: me dan por ganadora?
es que todo ocurrió sin darme cuenta. (ojito con las acotaciones).
un abrazo de
reichel.(como le dicen en el barrio)

alejo -

Confesá Pini!!

Después de explotar despiadadamente las cualidades del Excel durante un par de horas, he llegado a la segura conclusión que existe una sola solución al problema. En rigor de verdad existen 4, pero es la misma girada 90, 180 y 270 grados.

itn -

Lo del Quijote va en serio,
si lo crees... imprime, recorta y a girar y girar...hasta la 2ª solución encontrar. ;-)
Yo tambien pienso que pini es Raquel.

alejo -

Aclaremos que son 6144 posiciones si cambiamos las fichas de lugar, es decir 4x4x4x4x4!=6144
Dejando las fichas fijas en cada casilla nos da sólo 256 posiciones: 4x4x4x4=256
No tengo tiempo ahora, pero dudo que haya solución única (tanto sea para llevar la contra al dueño de casa).

Y si Pini respondió a la segunda pregunta, seguiré pensando que es Raquel.

itn -

pregunta.

itn -

Lo que si puedo hacer es felicitar a Pini, que por ahora es la única que ha resuelto la primera pregunta.
Brava Pini, bravissima.
¿o es la segunda?

itn -

Creo que es única, pero enviaré un ejemplar del Quijote al primero que me envié más de una solución.

En cuanto a la segunda pregunta creo que es muy difícil, más incluso que el P6 ya que, estoy con disinerge, habiendo 6144 posibles posiciones ahora tenemos que eliminar aquellas en las que alguna frontera coincida.

ramtia arrepentido -

Rectificamos mi solución para que el professor no me pongo un negativo.

Como una sola solución se puede rotar y canviar de posición en las otras casillas. Y solo he hallado una única solución que cumple con las figuras delante por delante.
Las soluciones montandolo bien son 4, luego si hacemos lo propio de antes tenemos:
Posibles soluciones 256 - 4 soluciones correctas = 252 soluciones en las cuales no estan emparejados los simbolos.

ramtia -

Si mis calculos no fallan, que seguro que estan mal. creo que son 255 soluciones.

Resolución: Suponemos que para que coincidan tiene una solución unica, por lo tanto todas las otras no coinciden.
Hay 256 soluciones posibles - 1 que es cierta=255 soluciones.

Seguro que son -10.

disinerge -

Estaré muy bajo de forma porque a bote pronto me salen 6144 posibles formas de colocar las fichas.

Ya solo con esa cifra me echo a llorar pero si leo "Visto qe eso es muy fácil..." deduzco que la solución con fronteras concordantes no es única (ni siquiera la busqué) porque encontrar una entre más de 6000 es como el gafe que se sienta en un pajar y se clava la aguja.

pini -

lo saqué.

alejo -

Si la respuesta es incorrecta son -10 puntos? je je.
Duro problema para las horas previas al IPST!, pero igual voy a arriesgarme por 208 soluciones. Seguro que está mal porque no estoy tomando en cuenta la simultaneidad de coicidencias.